Introduction

As we discuss about stormwater management, we have to bring up the topic of hydrology. This topic is studied by various disciplines. This module attempts to present the basis of engineering hydrology. It starts with the concepts of engineering hydrology and water balance and follows by rainfall-runoff processes, and hydrologic routing. Readers who are interested to learning about groundwater hydrology may want to do further readings in hydrogeology.

Engineering Hydrology

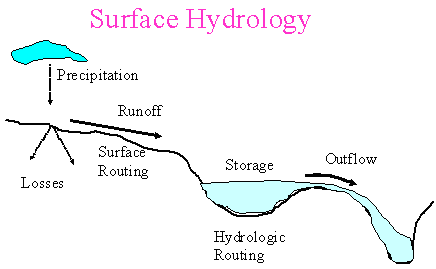
Hydrology encompasses the occurrence, distribution, movement, and properties of the waters of the earth. It involves the interaction of water with the physical and biological environment.

Hydrologic system is a system of interrelated components, including the processes of precipitation, evaporation, transpiration, infiltration, groundwater flow, streamflow, etc., in addition to those structures and devices that are used to manage the system. Hydrologic system is subject to different kind of weather pattern and spatial complexity, and is dynamic and random in nature.

Hydrologic evaluations are required to determine the characteristics of the hydrologic system including the evaluation of the magnitude of various events and the frequency of certain magnitudes.

Engineering hydrology is a Apractising art@ concerned with the analysis of hydrologic systems and hydrologic evaluations related to planning and design objectives. One of the major problems in engineering hydrology is the lack of measurement at the location of interest.

1. Statistical analysis of historic records
   Based on the analysis of past records of the system, the future behaviour of the system is estimated statistically. This approach assumes that land use, climate, vegetation, soil conditions, and other factors must all be static.
   
   
2. Extension of records
   For short records, theoretical models which are based on physical or statistical laws can be used to extend the existing data record.
   
   
3. Transferring of records
   If records are short or inadequate at a location of interest, previous records from a similar catchment may be used to predict the system behaviour. It is important that the system performance be related to a set of easily-measured characteristics.
   
   
4. Hydrological Modelling
   If records are short or inadequate at a location of interest, a mathematical model is used to simulate the hydrologic processes directly. The mathematical model transforms the inputs such as rainfall to output such as runoff or streamflow. This transformation may involve simple conceptual models to complex physically based models.
   

Hydrologic Budget

Hydrologist usually define regions of analysis using the concept of watershed. A watershed is the land area that contributes surface runoff to any point of interest. The hydrologic system components interact with each other and the processes involved are enormous and complex. Nevertheless, important watershed processes should be identified so that the hydrologic system can be analyzed adequately. Inputs to the hydrologic system are rainfall and/or a regional groundwater flow system while outputs are groundwater outflow from the region, receiving channel and stream flows, and evapotranspiration to the atmosphere. Hydrologic processes are a function of the characteristics of the study area such as climate, topography, geology, soil cover, vegetation, land use and human activity. Although watershed processes are complex, it may be represented in a simplified way. For instance, evapotranspiration is usually assumed negligible when floods are being simulated but must be included in studies of long-term reservoir operation.

If we can identify all the important inputs and outputs of a hydrologic system, a water budget analysis can be conducted which would give an estimate of the magnitude of hydrologic components. Hydrologic budget is usually applied to a well defined region. Watersheds are the easiest to deal with since they sharply define surface water boundaries.

In order to apply the hydrologic budget equation, we need to define a control volume or a region which is fixed in space and completely surrounded by a control surface through which matter can freely pass. By identifying all inputs and outputs through the control surface, a change of water inside the control volume can be computed using the following conservation equations:

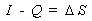
where I is the amount entering the region in a specified time period delta t, Q is the amount leaving, and delta S is the amount of change within the system.

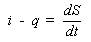
where i and q are the instantaneous input and output rates.

Although the concept of hydrologic budget is simple, the identification and quantification of inputs and outputs may be very complex.

Hydrologic budget equations can be developed for the surface system, subsurface system, and the combined system. The difficulty in solving these equations for practical problems lies mainly in the inability to measure or estimate properly the various hydrologic equation terms. Precipitation is measured by rain or snow gauges. Surface flows can be measured by weirs, flumes, velocity meters and depth gauges. Soil moisture can be measured using neutron probes and gravimetric methods. Infiltration can be determined locally by infiltrometers. The extent and rate of movement of groundwater are usually exceedingly difficult to determine and adequate data on quantities of groundwater are not always available. The determination of quantities of water evaporated and transpired is also extremely difficult.

One of the fundamental tools used in defining hydrologic response has been a water balance analysis. This type of analysis has historically been used to obtain an understanding of the overall hydrologic response of an area or watershed. While not generally being overly detailed, the analysis gives a basic understanding of the rainfall-runoff relationship over a long term planning period (e.g., seasonal or yearly). The outcome of such an analysis allows for the general breakdown of the components and their percentages which go into defining runoff from a site, surface and subsurface.

A typical water balance analysis will compare meteorological input data to a measured (or transferred) set of flow data within the receiving stream. The analysis of the streamflow over time allows for this data to be broken down into surface runoff and ground water or baseflow components. The flow data along with typical estimates of evapotranspiration losses and the input meteorological information allows for breakdown of each component and a determination of infiltration, baseflow and the surface flow components of individual site water balance.

A water balance (or hydrologic budget) analysis gives information which can be useful from a series of planning or analytical perspectives. At a watershed level of planning, a watershed manager can determine on an annual or seasonal basis the general volumes and percentages of precipitation which is being runoff directly into the surface streams and the percentage of streamflow which can be attributed to baseflow and ground water. This information can assist in determining the potential sensitivities of the watershed to alteration features which may affect these functions (e.g., land use change, climate change).

From a watershed management perspective, a water balance analysis is useful in establishing some of the broad level issues which may exist within the watershed and assisting in setting direction for further detailed assessments or policy development.

The relative percentage of surface runoff to rainfall input is useful in establishing the volumetric parameters required to effectively calibrate and verify the more detailed hydrologic modeling. The information developed regarding the baseflow characteristics of the watercourses and the percentage of meteorological input which feeds this hydrologic component can be used be used in defining fisheries and geomorphologic directions for watershed level of study.

Rainfall

Most of us are aware of the saying AGarbage in, garbage out@. In engineering hydrology, the input to the hydrologic cycle is precipitation. Hydrologic analysis cannot be performed with confidence until we believe the input precipitation is adequately measured in both the spatial and temporal dimensions. Nevertheless, accurate measurement of precipitation does not mean extensive gauging stations and endless amount of resource. By designing a suitable gauing network, the precipitation of a region of interest may be estimated reasonably.

Precipitation is derived from atmosphere water, its form and quantity is influenced by climatic factors such as wind, temperature, and atmospheric pressure. There are different forms of moisture falling from the atmosphere to earth: drizzle, rain, glaze, sleet, snow, snow pellets, and hail.

Precipitation is produced primarily when the water vapour in the atmosphere becomes saturated, condenses and increases in weight such that solid or liquid water can no longer be supported by up-drafts and other air currents and fall to the earth surface.

The following three conditions are required in order to produce precipitation:

1. A continuous supply of water vapour through evaporation and transpiration processes and the air movement to transport the water vapour to the location of rainfall.
   
   
2. Nucleating particles such as dust, salt, pollen, and various atmospheric ions for condensation must be present.
   
   
3. A cooling mechanism sufficient to cause condensation and growth of water droplets or ice crystals from water vapour.

A number of rain gauges are commonly used for measuring rainfall. They are:

1. Non-recording storage gauge
   This gauge can only record periodic volume of rainfall such as daily rainfall. It cannot be used to indicate the time distribution of rainfall.
   
   
2. Recording weighing gauge
   It operates by continuously recording the weight of the accumulated rainfall. Data are either recorded on tape or transmitted to remote data gathering station.
   
   
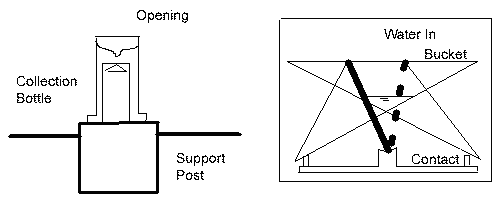
3. Recording tipping bucket gauge (See the following figure)
   It senses each consecutive rainfall accumulation when it reaches a prescribed amount usually 0.01 in or 1 mm of rain. A small calibrated bucket is located below the rainfall entry port of the gauge. When it fills to the 0.01 in or 1 mm increment it tips over, bring a second bucket into position. These two small buckets are placed on a swivel and the buckets tip back and forth as they fill. Each time a bucket spills it produces an indication on a strip chart or other recording form. A record of rainfall depth versus time is produced.
   
   
   
4. Radar
   It is used to estimate rainfall intensity because it can detect any type of raindrops in the atmosphere. The reflection of the raindrops is determined by electromagnetic energy of the radar pulse, called echo. The brightness of the echo is a measure of the rainfall intensity. The strength of reflected radar pulses is a function of the number and size of the raindrops. As a result, it can detect light, medium, intense and very intense rainfall. Because of interference such as building and trees, it should be used together with rain gauges to provide estimate for areas not covered by rain gauges. The Meteorological Services of Canada (MSC) operates 14 weather radars across Canada.
   
   
5. Satellite
   The principal value of remote sensing is its ability to provide regional coverage and point measurement. Additionally, satellite communications can be digitized and transfered to computer for analysis and presentations.

MSC also has real time access to digital imagery from both geostationary and polar orbiting satellites launched by agencies in the U.S.

Monitoring networks are used to determine the spatial and temporal distribution of rainfall and snow in a regional setting. The spatial variation of precipitation is due to the fact that precipitation events are dynamic and moving constantly. The temporal aspect of precipitation is signficant for rainfall of short and long duration. As the costs of monitoring can be very high, monitoring networks should be designed to be efficient and cost-effective. In order to design a cost-effective monitoring network, the designer should have a comprehensive knowledge of the system to be monitored, the data to be used, and the level of detail in space and time.

In Canada, the MSC publishes precipitation data. Other sources include private companies, municipal networks and other government agencies.

The minimum precipitation-gauge densities recommended by the World Meteorological Organization (1974) for various climatic situations are shown in the following table. In Canada, the target density is about 25 km separation between standard precipitation gauges and there are about 200 recording rain gauges. The national network provides large-scale and long-term records of precipitation and other meteorological information, which may be used for the planning and design of water resources structures on a regional scale. In Ontario, there are currently about 50 recording rain gauges in operation.

For mountainous setting, a higher density of gauging stations is usually required to monitor the patterns of precipitation and irregularities based on topography.

The number of rain gauges required for watershed monitoring depends on the nature of rainfall, topography, and the level of analysis (e.g., flooding, water balance). Typically, lower density of rain gauges is required to get representative measurements for long periods or larger areas. For individual rainfall event measurement, the rain gauge density may be very high (e.g., 5 km2/gauge). Measurement of daily rainfall over an area typically requires much lower rain gauge density (e.g., 18 km2/gauge).

The approximate lengths of records necessary to achieve stable frequency distributions are:

1. Mountains - 50 years
2. Plains - 40 years
3. Coastal - 30 years

When we have collected rainfall data from multiple gauges, the average depths for the whole area can be estimated by a number of techniques: (1) arithmetic average method; (2) Thiessen Method; and (3) Isohyetal method.

1. Arithmetic Average Method
   This method uses the sum of all precipitation values and divides by the total number of gauges used. Although this is the simplest method, it is also the least accurate. It may be satisfactory if gauges are uniformly distributed and the topography is flat.
   
   
2. Thiessen Method
   In this method, all the gauge locations are plotted on the map at an appropriate scale. Next, straight lines are drawn to connect gauges without crossing any other lines. Each connecting line is then bisected and a perpendicular is drawn through the connecting line. Each gauge is near the centre of a polygon whose size varies according to the spacing of the gauges. The area of each polygon is then measured and the percentage of the total area for each polygon is then computed. Finally, the average rainfall over the basin (Pavg) is computed as
   
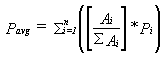
   where Ai is the area of each polygon and Pi is the rainfall data at the centre of each polygon, and n is the total number of polygons. This method is not suitable for mountainous areas because of orographic influences.
   
   
3. Isohyetal Method
   In this method, the rainfall values are used to develop a contour plot. The average precipitation is calculated between isohyets (or contour lines) by taking the mid-value between two successive contours. The area between each successive isohyets is found by either measuring with a planimeter or counting grid squares. The average rainfall over the basin (Pavg) is computed as
   
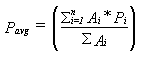
   where Ai is the area between contours and Pi is the rainfall data between isohyets, and n is the total number of areas. This method is perhaps the most accurate approach for estimating average rainfall.

Meteorological data can be described by both average observation and extreme events such as floods and droughts. In order to transform the large meteorological database into some useful value for planning and design purposes, hydrologists apply statistical techniques to record data.

The statistical problems in hydrology are usually associated with the frequencies with a set of observations. The frequencies of extreme rainfall events are termed as return period, that is, the average interval of time between events which equal or exceed the magnitude of the event of interest.

This section introduces three types in rainfall analysis: storm event analysis; intensity-duration-frequency curve; and probable maximum precipitation.

1. Rainfall Hyetograph and Storm Event Analysis
   
   Rain is usually measured in incremental volumes at gauging stations. These increments take the form of daily volume, or volume at some other increment of time. It is possible to plot the rainfall volume, or its equivalent the rainfall intensity, for incremental times during the event. The result is a plot known as a hyetograph. The shape of the hyetograph for a particular rainfall event constitutes the time history of that event.
   
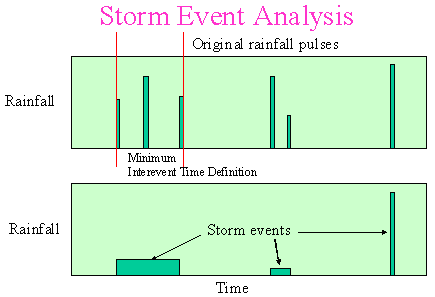
   A hyetograph can be used in single event and continuous simulation anlaysis of rainfall-runoff processes. A long-term continuous hyetograph consists of a series of rainfall pulses through time. To separate it into independent storm events, a definition of the minimum interevent time is required; the reason for this being so that any two pulses of rainfall can be considered to be belonging to separated events if the time period between the pulses is longer than the minimum interevent time. Storm event analysis can be used to determine the statistics and the probability distributions of rainfall volume, duration, average intensity, and interevent time from a long-term hyetograph. Analysis of a number of rainfall record across Canada (Adams et al, 1983) indicates these characteristics can be described as exponential density functions. Such statistical information can be used in statistical analysis of rainfall-runoff process (Adams and Bontje, 1983).
   
   
   
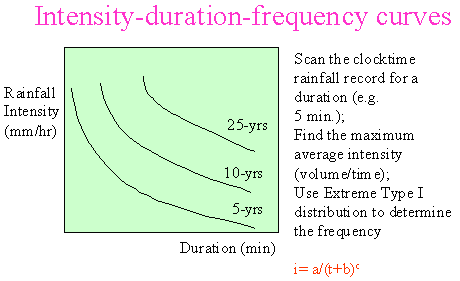
2. Rainfall Intensity-Duration-Frequency Curves
   
   An observed hyetograph is useful as an indication of the severity or typical nature of rainfall events, and in calibration of models. However, a natural event often has little intuitive significance and no discernable probability, since there are no two events that are identical. It is therefore useful to seek alternatives to the direct use of observed rainfall events.

   The most basic definition of a storm event lies in its duration and volume, and possibly in its peak intensity. In the long term, rainfall can be assessed according to the frequency of a given duration and volume occurs. This relationship is defined by curves known as Intensity/ Duration/ Frequency (IDF) curves.

   To generate an IDF curve, observed rainfall records are scanned for all instances of a particular combination of duration and volume; the number of times that combination occurs provides a measure of likelihood. Assessing the problem in terms of the number of times a combination is exceeded, provides a probability that expresses the frequency of exceedance of that combination. Compiling statistics for all combinations leads to curves that define the relationship between rainfall event intensity, duration, and frequency.

   The MSC defines an intensity-duration event for a particular duration, to, as the annual maximum intensity determined. The duration selected are arbitrary time periods over which rainfall is totalled and are not necessarily related to the physical duration of a storm. The MSC types IDF curves are derived by scanning the clocktime rainfall record with the event definition: t<=to, annual max i=(v/to). The extreme annual series is determined, and a Type 1 extreme value distribution is used to calculate the frequency of intensity and duration.
   
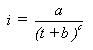
   where

   i	=	intensity (mm/hr)
   t	=	time in minutes
   a, b, c	=	constants developed for each IDF curve

   
   Once an IDF relationship is developed for the area of interest, a certain combination of design intensity and duration can be determined for a particular frequency of occurrence. The IDF curves are used extensively in single event analysis of rainfall-runoff processes.
   
   
   
   
   
3. Probable Maximum Precipitation (PMP)
   The probable maximum precipitation is the critical depth-duration-area rainfall relation for a given area and season which would result from a storm containing the most critical meteorological conditions considered probable.

   These critical conditions are determined by the analysis of effective precipitable water, depth of inflow layer, wind, temperature and other factors, and the historical record of extreme storm events in the region, topography, season, and location of the area.
   

Hydrologic Losses

Not all rainfall events generate runoff directly. Minor rainfall events may be retained completely by aboveground objects such as trees and structures, soil infiltration, and surface depression. In order to estimate the direct runoff from rainfall events, it is important to understand the loss processes and quantify the amount of losses. Unfortunately, these losses are usually very difficult to quantify the amount and they vary across time and space. For practising hydrologists and engineers, some form of approximation of the hydrologic losses may be required. These approximation may be based on actual field measurement, previously reported data from similar catchments, and computer simulation of the physical processes involved.

Interception refers to the precipitation that wets and adheres to aboveground objects such as trees and buildings and finally returns to the atmosphere through evaporation. It is a function of storm eharacter, the species, age and density of prevailing plants and trees, and the season of the year.

Usually about 10-20% of the precipitation that falls during the growing season is intercepted and returned to the hydrologic cycle by evaporation. Interception during rainfall events is commonly greater than for snowfall events. Estimates of losses to gross precipitation through interception can be significant in annual or long-term models, but for heavy rainfalls during individual storm events, accounting for interception may be unnecessary.

Most interception loss occurs during the initial storm period and the rate of interception rapidly decreases to zero. In addition to trees, forms of vegetation can also intercept large quantities of water.

Depression storage refers to the precipitation which is trapped in numerous small depressions. It is a function of the land form and local land-use properties and it varies widely in size, degree of interconnection, and contributing drainage area. Depressions can be considered as small reservoirs. Depression storage is sometimes assumed to be a constant throughout the storm events. Rainfall is assumed to fill up depression storage before runoff begins.

Water evaporation can be from the soil as well as open water bodies to the atmosphere. This is a significant process in the hydrologic cycle because it supplys the atmosphere with water moisture for the subsequent rainfall events. It is significant over large bodies of water such as lakes, reservoirs, and the ocean.

Evaporation occurs when a molecules of water moves quickly enough to break away from other water molecules at the water-air interface. In order for the water molecules to break away, the latent heat of evaporation (540 calories per gram of water at 100 C) is required. Water molecules also enter the water from air through the condensation process. The net exchange of water molecules at the air-water interface is determined by the rate of evaporation and the rate of condensation. Evaporation will proceed when suffieient energy is available (e.g., heat in water or solar radiation) and when the vapour pressure above the water is less than the saturation vapour pressure.

Evaporation from water surface is a function of

1. Solar radiation
   Solar radiation provides energy that can be stored as heat in the water. This latent heat is transformed to kinetic energy as water molecules evaporate.
   
   
2. Temperature
   Although temperature is not directly related to evaporation rate, it controls the saturation vapour pressure and affects the difference in vapour pressure between the surface and the bulk air above.
   
   
3. Humidity
   The rate of evaporation is directly proportional to the difference between actual humidity in the air above the water the saturated humidity that occurs at a specified temperature.
   
   
4. Wind
   Wind can remove the more humid air above the water surface and replace it with dry air that enhances the rate of evaporation. However, the maximum evaporation rate is controlled by factors other than wind speed and increasing wind speed above a certain value would cause no increase in evapoation.
   
   
5. Water body depth
   Shallow lakes warm up more quickly and follow seasonal temperature trends more closely than do larger lakes. Shallow lakes with a small water volume show high evaporation rates during summer months and lower evaporation rates during the winter period. However, deep lakes with large volumes generally lay behind atmospheric temperature trends and have sufficient water volume to release the stored energy in cooler months, permitting evaporation in the absence of sufficient solar radiation. Higher evaporation rates may occur in winter months rather than in summer months in large lakes.
   
   
6. Size and shape of water surface
   As dry air travel across a large lake, the vapour pressure or water content of the air will begin at low values on the windward side of the lake and become progressively more humid as it proceeds across the lake surface. Evaporation rates will be highest on the windward side of the lake but will decrease as the air mass moves across the lake and the relative humidity increases.
   
   The average rate of evaporation over a lake will depend on the relationship between the prevailing wind direction and the orientation of the long axis of a lake. If the prevailing wind moves along or parallel to the long axis of a lake, the vapour pressure will increase to a greater content and therefore the rate of evaporation will decrease towards the leeward side of the lake. As a result, the maximum rate of evaporation from the lake occurs when the air mass is in contacct with the lake for the shortest period. If the prevailing wind crosses the lake along the short axis, the air does not pick up as much moisture and the rates of evaporation remain higher.
   
   
7. Water quality
   Evaporation from a free water surface will decrease proportionally to increasing salintiy. For instance, if the total dissolved solids of the water increases by 1%, the evaporation form that water will decrease by 1%. This caused by the tendency of dissolved ions in water to hold water molecules more closely together.
   

Evaporation from soils is a function of

1. Soil moisture content
   This is the most significant factor. As the moisture content of the soil decreases, the evaporation rate will decrease as the dry soil on top acts as a barrier to provent evaporation of water at greater depth.
   
   
2. Water table depths
   Maximum evaporation rates will occur when the water table is at the ground surface. As the water table depth increases, the rate of evaporation decreases.
   
   
3. Soil characteristics
   Soil characteristics affect the rate of evaporation and the availability of water to evaporate. In general, fine-grained soils hold more moisture and have a greater reservoir of water for evaporation. Additionally, the finer-grained soils have a greater capillary effect and transport water from greater depths to be evaporated at the surface. As a result, areas with fine-grained soils are subject to greater evaporation than areas with coarse-grained soils.
   
   
4. Soil colour
   Materials with a darker colour absorb more solar radiation than ligher-coloured materials. Dark soil will absorb more energy and be subject to greater evaporation rates than light soils.
   
   
5. Vegetative cover
   Vegetative cover tends to decrease the amount of evaporation compared to that of a vare soil. Plants provide shade on the soil surface and decrease the amount of solar radiation reaching the ground. Plants also provide a wind block that reduce the wind speed at the soil surface and reduce evaporation rates. Plant can also increase the relative humidity close to the ground surface through transpiration and decrease simple evaporation from the soil surface.
   
   For open bodies of water, evaporation can be 100% while for soils it varies from a high 100% when the soil is highly saturated to essentially zero at stages of very low moisture content

Transpiration is the evaporation of water from the vascular system of plants into the atmosphere. Water is taken up by plant roots in the soil, moves to the branches and leaves where evaporation takes place. The amount of water used for plant growth is negligible compared to the water that is transpired. Transpiration occurs not because the plant is breathing, but because of the difference in vapour pressure inside the leaf and in the air outside.

Transpiration is controlled by the same factors that control simple evaporation from water surface. These include:

1. Solar radiation
   The solar radiation to plant leasves controls the opening of the stomata and controls transpiration. Maximum transpiration rates occur during daylight hours and in the summertime with minimum rates at night and cooler weather.
   
   
2. Air temperature
   Transpiration shows a maximum rate at an optimum temperature of a plant species.
   
   
3. Air humidity
   The difference in vapour pressure within the stomatal cavities of the leaves compared to the vapour pressure in the outside air is a driving force for transpiration.
   
   
4. Wind and air turbulence
   Wind and air turbulence removes the saturated air and increase the vapour pressure gradient between the air inside the leaves and the surrounding air.
   
   
5. Vegetation
   When stomata are closed, virtually no transpiration can occur. When they are open, the climatic factors control the rate of evapotranspiration. Length of daylight, air temperature, and higher humidity control the length that stomata remain open.
   
   Lighter colour for plant leaves reflect solar energy and reduces transpiration. The more dense a vegetative cover, the more leaf surface area will be available for transpiration. Broader leaves provide greater surface area for evaporation. Transpiration will increase with the growth of plant. Plants with deep root types supply more water for transpiration.
   
   
6. Soil moisture content
   The availability of moisture in the soil zone will control the amount of tranpiration that can occur.
   
   
7. Storage capacity
   Fine-grained materials will store more water than coarse-grained materials. As a result, more water is available in fine grained soils.
   
   
8. Capillary tension
   Finer-grained soils can hold greater amounts of water by capillary action than coarse-grained soils.
   
   
9. Soil permeability
   Higher soil permeabilities permit faster replenishment of water to the root zone and lower permeabilities decrease the rater of replenishment.
   
   
10. Depth to the water table
    The depth of the root zone for different plants ia a very important controlling factor for evaporation. The change in water levels as a result of plant uptake of water can be used as a direct measurement of evapotranspiration rates.
    

Potential evapotranspiration is the rate at which evapotranspiration would occur from a large area uniformly covered by vegetation with unlimited access to soil water and disregarding heat flow and storage effects. It cannot exceed free water evaporation under similar climate.

Infiltration is the entry of waters into the ground. The rate and quantity of water which infiltrates is a function of soil type, soil moisture, soil permeability, ground cover, drainage conditions, depth of water table, and intensity and volume of precipitation (Wanielista et al. 1997). The infiltrated water replenishes soil moisture, recharges groundwater aquifers, and ultimately augment base flow in streams.

After water crosses the surface interface, its rate of downward movement is controlled by the transmission characteristics of the underlying soil profile. The volume of storage available below ground is also a factor affecting infiltration rate. The major influencing factors of infiltration are soil type and moisture content. The soil type characterizes the size and number of passages through which the water must flow while the moisture content sets the capillary potential and relative conductivity of the soil.

Infiltration, together with other hydrologic losses, determines the rate of runoff from a catchment.

Runoff

Runoff analysis is a very important component of surface hydrology. Although the process appears to be simple as it occurs frequently around us, the relationship between precipitation and runoff is affected by various storm and basin characteristics and is very complex. Various techniques which range from simple lumped models to sophisticated continuous simulation models have been developed for runoff prediction. Simple lumped models may be suitable for planning analysis of runoff while continuous simulation may be appropriate for design analysis.

Runoff occur when precipitation exceeds the hydrologic losses. It starts with overland flow which is then collected and transported by various drainage pathways such as streams and storage reservoirs and eventually discharged to receiving water bodies such as rivers and lakes. The precipitation-runoff process is complex as it involves numerous flow routing interactions in the watershed. Additionally, the spatial and temporal characteristics of precipitation also make the prediction of runoff a challenge to engineers.

Watershed characteristics which affect runoff include:

1. Stream patterns
   Stream patterns affect the pathways of runoff at a watershed. Runoff from different parts of a watershed will interact with each other in accordance with their runoff pathways
   
   
2. Geomorphology of drainage basins
   Both large scale and local geologic activity and structure affect the storage and movement of surface waters. The nature of land forms determines drainage pattern which in turn also affects the surface geometry through the process of erosion.
   
   
3. Overland flow lengths and stream lengths
   Overland flow length is the distance from the ridge line or drainage divide, measured along the path of surface flow which is not confined in any defined channel, to the intersection of this flow path with an established flow channel.
   
   The flow length to any point is the sum of overland flow lengths and stream lengths. The flow length is important in the application of Rational Method of runoff peak calculations.
   
   
4. Areal characteristics
   Drainage area has been used as a parameter in regression models of precipitation-runoff process. As drainage basins increase in size, they become longer and narrower. Drainage density is defined as the ratio of total channel segment lengths cumulated for all stream orders within a basin to the basin area.
   
   
5. Channel and Basin Gradients
   The slopes of a drainage basin and its channels have a strong influence on the runoff process as they affect the runoff rate
   
   
6. Area-elevation relation
   The distribution of area between contour in a drainage basin is an important characteristics as it relates to the storage and flow characteristics of the basin.
   

A stream hydrograph is a continuous plot of discharge rate versus time at a point along a stream during a storm event. Streamflow is usually measured by stage (i.e., depth). Therefore, it starts with the plot of stage versus time. Then, it is transformed into flow versus time using a rating curve (i.e., stage-discharge curve) at the point of measurement.

Streamflow hydrographs provide information on peak flows, time distribution of flows, the total flow volume over a certain duration which can be used to determine flooding potential and size reservoirs, storage tanks, detention ponds, and other facilities.

A hydrograph has four components:

1. direct surface runoff;
2. interflow
3. groundwater or base flow;
4. channel precipitation.

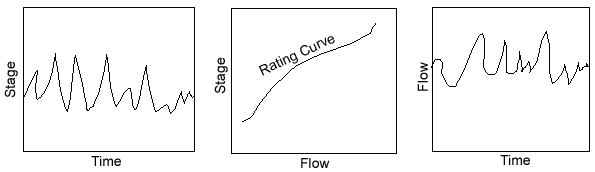
The rising limb is called concentration curve, the region in the vicinity of the peak is called the crest segment, and the falling limb is called the recession curve. The shape of a hydrograph is a function of precipitation pattern characteristics and basin properties.

In general, there is a baseflow component which are considered to be normal day-to-day flow. The runoff component can be divided into the abstraction and direct runoff. If baseflow and abstraction are removed from the streamflow hydrograph, the resulting hydrograph is called direct runoff hydrograph. The main component to be separated from the streamflow hydrograph is the baseflow.

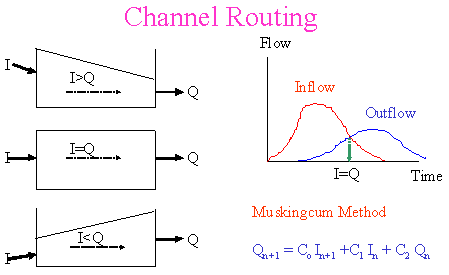
There are two main approaches in modelling rainfall to runoff. Deterministic models assume the same inputs will produce the same outputs. On the other hands, stochastic models assume both inputs and outputs are random variables and the same inputs may produce different outputs. However, the preferable modelling approach is a function of time, budget, expertise of the users and the purpose of the analysis. The following diagram shows two common deterministic models for rainfall-runoff transformation.

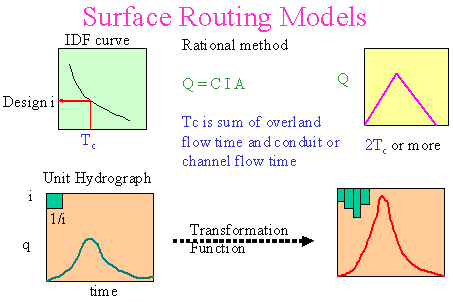
Hydrologic Channel Routing

Hydrologic routing is used to simulate the temporal and spatial variations of a flood wave as it traverses a river reach or detention reservoir. In hydrologic routing, the equation of continuity and a linear or curvilinear relation between discharge and storage within a river and reservoir are used.

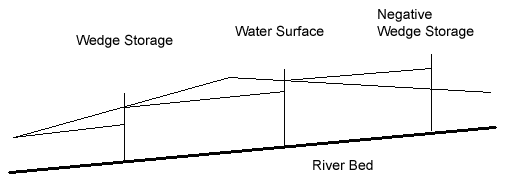
When a flood wave enters a river section, the water surface within the section is not always parallel to the channel bed. The storage in a channel can be considered as a combination of prism storage and wedge storage as shown in the following figure. The prism storage is the volume of water that would exist if the flow were uniform at the downstream depth. The wedge storage is the volume of water between the actual water surface profile and the top surface of the prism storage. The wedge storage increases the flood volume during the rising stage and decreases it during the receding stage. Thus, the storage-discharge curve of the river section is a loop reflecting the rising and falling stages. Additionally, local inflows and seepage within the river section should be accounted for in hydrologic river routing.

Hydrologic river routing are all based upon the following equation of continuity:

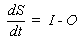
where I is the inflow rate to the reach; O is the outflow rate from the research; and (dS/dt) is the rate of change of storage within the reach. This lecture introduces the Muskingum Method.

Muskingum Method
In order to solve the above equation, a relationship between storage and inflow and outflow is required. This method utilizes the following relationship:

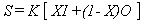
where K is the storage time constant for the reach and X (or c in the textbook) is a weighting factor that varies between O and S. Substituting Eq. (2) into Eq. (1) and denote subscripts 1 and 2 as the beginning and ending times, Eq. (1) becomes

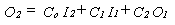
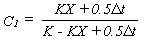
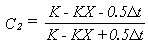
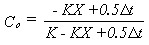
Values of K and X (or c in the textbook) for this method are commonly estimated using K equal to the travel time in the reach and an average value of X equal 0.2. If inflow and outflow hydrograph records are available, they can be used to estimate K and X.

This method works best for

• slowly changing flows,
• streams with small slopes where the storage-discharge curve is approximately linear,
• delta t is much smaller than the travel time of flood wave and small enough to ensure linear variation of inflows and outflows. A rule of thumb of delta t is given by

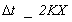
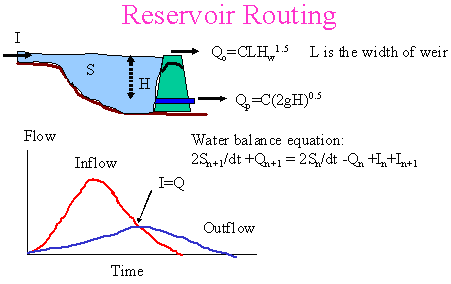
Hydrologic Reservoir Routing

A flood wave which passes through a storage reservoir is delayed and attenuated as it enters and spreads over the reservoir surface. Water that is stored is then released through either a controlled or uncontrolled outlet. To route a flood wave through a nonlinear reservoir, the storage-outflow relation and the continuity equation are combined to determine outflow and storage at the end of each time step. Thus, both the elevation-storage curve and elevation-discharge curve must be developed.

Elevation-storage relation can be estimated by

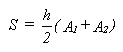
where A1 is the surface area of the reservoir when h equals zero and A2 is the surface are of the reservoir when h equals the depth of flow.

Elevation-discharge curve is assumed to be unique for a reservoir and is described by the following equations:

1. Uncontrolled weir outflows
   
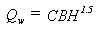
   where Qw is the weir discharge rate; C is the weir coefficient; B is the weir length; and H is the hydraulic head above the weir crest.
   
   
2. Controlled orifice outflows
   
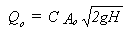
   where Qo is the orifice discharge rate; C is the orifice coefficient; Ao is the orifice area; g is the gravitational constant (9.81 m/s2); and H is the depth of water above the centre line of orifice.

The hydrologic volumetric balance equation can be rearranged as follows:

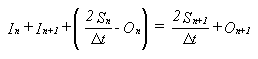
where the unknowns are the terms on the right side. Routing time (delta t) should not be too short or too long.

The procedure for hydrologic reservoir routing is listed below:

1. Develop elevation-storage and elevation-discharge curves and combine them to a storage indication curve (i.e., a plot of (2S/delta t + O) versus O).
   
   
2. Knowing In, In+1, Sn, and On, compute the left hand side of Eq. (11), i.e., (2Sn+1/delta t + On+1).
   
   
3. Determine On+1 from the storage indication curve (i.e., a plot of (2S/delta t + O) versus O).
   
   
4. Compute (2Sn+1/delta t - On+1) by substracting 2On+1 from (2Sn+1/delta t + On+1).
   
   
5. Add In+1, In+2 and (2Sn+1/delta t - On+1) to determine the left hand side of Eq. (11) and to back to step (3) for the next time step.